Estatística de Fermi-Dirac

Em mecânica estatística, a estatística de Fermi-Dirac é uma estatística quântica que descreve o comportamento de sistemas de partículas com spin semi-inteiro, os férmions. Leva o nome de dois eminentes físicos: Enrico Fermi e Paul Adrien Maurice Dirac cada um dos quais descobriu o método de forma independente (embora Fermi tenha definido as estatísticas antes de Dirac). Antes do estudo da estatística de Fermi-Dirac é necessário compreender algumas diferenças entre sistemas clássicos e quânticos. Sistemas clássicos são formados, a priori, por partículas distinguíveis, ou seja, é possível identificar e diferenciar tais partículas individualmente e nestes sistemas os efeitos quânticos são desprezíveis, sendo o sistema descrito pela estatística de Maxwell–Boltzmann. Já sistemas quânticos são formados por partículas indistinguíveis, devido à superposição de suas funções de onda, ou seja é impossível descrevê-las individualmente e neste sistema os efeitos quânticos devem ser considerados. Sistemas quânticos podem ser descritos pelas estatísticas de Fermi-Dirac ou de Bose-Einstein, dependendo do spin das partículas.

Distribuição de Fermi-Dirac em função de ε/μ para quatro temperaturas diferentes.

Formulação matemática

Como as partículas são indistinguíveis na estatística de Fermi-Dirac, a especificação do número de partículas é suficiente para determinarmos o estado do gás. Como os férmions obedecem ao princípio de exclusão de Pauli, não é possível que mais de uma partícula esteja no mesmo estado, se faz apenas necessário somar sobre todos os números possíveis de partículas em um único estado, ou seja, os dois possíveis valores :

$n_{r}=0,1$ para cada $r$

Quando o número total de partículas $N$ é fixado, a soma sobre todos os valores possíveis de $n_{r}$, com $n_{1},n_{2},...$ segue a seguinte relação

$\sum _{r}n_{r}=N$

Dado um sistema com $N$ férmions em equilíbrio térmico a uma temperatura arbitrária $T$, o número médio de partículas $<n_{s}>$ em um estado particular $s$ com energia $\epsilon _{s}$ é obtido através da distribuição canônica, logo

$<n_{s}>={\frac {\sum _{n_{s}}n_{s}e^{-\beta n_{s}\epsilon _{s}}\sum _{n_{1},n_{2},...}e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+...)}}{\sum _{n_{s}}e^{-\beta n_{s}\epsilon _{s}}\sum _{n_{1},n_{2},...}e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+...)}}}$

no qual $\beta ={\frac {1}{k_{B}T}}$, sendo $k_{B}$ a constante de Boltzmann. Podemos renomear alguns termos na expressão acima, de forma que obtemos

$Z_{s}(N)=\sum _{n_{1},n_{2},...}e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+...)}$

Somando sobre $n_{s}$ = 0 e 1, temos

$<n_{s}>={\frac {e^{-\beta \epsilon _{s}}Z_{s}(N-1)}{Z_{s}(N)+e^{-\beta \epsilon _{s}}Z_{s}(N-1)}}$

ou, ainda, podemos simplificar:

$<n_{s}>={\frac {1}{[Z_{s}(N)/Z_{s}(N-1)]e^{\beta \epsilon _{s}}+1}}$

Na condição em que $\Delta N\ll N$, podemos escrever

$lnZ_{s}(N-\Delta N)=lnZ_{s}(N)-{\frac {\partial lnZ_{s}}{\partial N}}\Delta N=lnZ_{s}(N)-\alpha _{s}\Delta N$

$Z_{s}(N-\Delta N)=Z_{s}(N)e^{-\alpha _{s}\Delta N}$

com $\alpha _{s}={\frac {\partial lnZ_{s}}{\partial N}}$. Como $Z_{s}(N)$ é uma soma sobre muitos estados, a variação de seu logaritmo com o número de partículas total $N$ não é afetado por qual estado particular $s$ foi omitido no somatório. Portanto, podemos fazer uma aproximação em que $\alpha _{s}$ é independente de $s$:

$\alpha _{s}=\alpha$

Ainda, podemos aproximar $\alpha$ em termos da derivada da função partição $\mathrm {Z} (N)$ sobre todos os estados, assim:

$\alpha ={\frac {\partial ln\mathrm {Z} }{\partial N}}$

Se utilizarmos $\Delta N=1$ na aproximação, encontraremos a distribuição de Fermi-Dirac:

$<n_{s}>={\frac {1}{e^{\alpha +\beta \epsilon _{s}}+1}}$

Ainda, o parâmetro $\alpha$ pode ser determinado pela primeira condição feita nesta dedução, em que

$\sum _{r}<n_{r}>=N$

ou

$\sum _{r}{\frac {1}{e^{\alpha +\beta \epsilon _{r}}+1}}=N$

Da relação entre a função partição $Z$ e a energia livre de Helmholtz $F$, sabemos que $F=-k_{B}Tln\mathrm {Z}$, logo:

$\alpha =-{\frac {1}{k_{B}T}}{\frac {\partial F}{\partial N}}=-{\frac {\mu }{kT}}$

$\alpha =-\beta \mu$

onde $\mu$ é o potencial químico. Então outra forma de se definir a distribuição de Fermi-Dirac é:

$<n_{s}>={\frac {1}{e^{\beta (\epsilon _{s}-\mu )}+1}}$

Quando os níveis de energia são muito próximos, de modo que podemos considerar que formam um contínuo, o número médio de partículas com energia entre $\epsilon$ e $\epsilon +d\epsilon$, pode ser escrito como

$n(\epsilon )=g(\epsilon )F(\epsilon )d\epsilon$

Onde $g(\epsilon )$ é a densidade de estados, de modo que $g(\epsilon )d\epsilon$ fornece o número de estados com energia entre $\epsilon$ e $\epsilon +d\epsilon$. E $F(\epsilon )$ é a chama função de Fermi, dada por

$F(\epsilon )={\frac {1}{e^{(\epsilon -\mu )/k_{B}T}+1}}$

Interpretação física

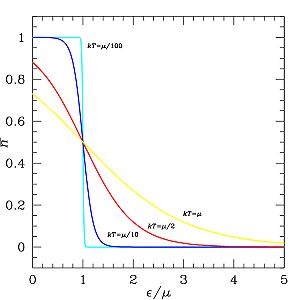
Para uma temperatura de 0 K, a função de Fermi é uma função de passo que vale 1 se $\epsilon <\mu$ e 0 se $\epsilon >\mu$. Ou seja, todos os estados com energia $\epsilon <\mu$ estão ocupados, enquanto os estados com energia $\epsilon >\mu$ estão vazios. A energia do último nível ocupado em 0 K se denomina energia de Fermi ($\epsilon _{F}$) e corresponde ao potencial químico do sistema. Também é usual associar uma temperatura a esta energia mediante $\epsilon _{F}=k_{B}T_{F}$, sendo $T_{F}$ a temperatura de Fermi.

No entanto, a definição mais precisa para a energia de Fermi é de que se trata da energia para a qual a função de Fermi é igual a 1/2, independentemente da temperatura. Deste modo, a energia de Fermi possui uma dependência com a temperatura embora muito fraca. Termodinamicamente, esta definição ainda equivale ao potencial químico do sistema.

À medida que a temperatura do sistema aumenta, as partículas nos estados ligeiramente abaixo do nível de Fermi (até cerca de $\epsilon _{F}-k_{B}T$) são excitadas para estados com $\epsilon >\epsilon _{F}$ (até $\epsilon _{F}+k_{B}T$), e a função de Fermi deixa de ser uma função de passo e se apresenta mais suave, como pode ser visto na Figura 1. Estados com energias menor que $\epsilon _{F}-k_{B}T$ não são excitados em consequência do princípio de exclusão de Pauli, uma vez que a energia adquirida os levaria aos estados já ocupados.

A distribuição de Fermi-Dirac tem importância capital no estudo de gases de férmions e em particular no estudo dos elétrons livres em um metal.

Aplicações

Conforme comentado anteriormente, as estatísticas de Fermi–Dirac e Bose–Einstein são aplicadas quando efeitos quânticos são apreciáveis e as partículas são consideradas "indistinguíveis". Os efeitos quânticos aparecem se a concentração de partículas (N/V) ≥ n_q (aonde n_q é a concentração quântica). A concentração quântica é atingida quando a distância média entre partículas é da ordem do comprimento de onda térmico de de Broglie, i.e. quando as funções de onda das partículas se superpõem.

Em decorrência disto, as partículas se tornam indistinguíveis e os resultados obtidos para qualquer grandeza mensurável não pode depender da identificação da partícula. Como a concentração quântica depende da temperatura; altas temperaturas irão colocar a maioria dos sistemas no limite clássico, desde que não possuam uma densidade muito alta, e.g. uma anã branca.

A estatística de Fermi–Dirac é aplicada a férmions (partículas com spin semi-inteiro que obedecem ao princípio de exclusão de Pauli) uma vez que sistemas constituídos de férmions devem ser descritos por uma autofunção total antissimétrica, o que implica na impossibilidade da existência de duas ou mais partículas ocuparem o mesmo estado; enquanto a estatística de Bose–Einstein é aplicada a bósons (partículas com spin inteiro). Tanto Fermi–Dirac quanto Bose–Einstein tornam-se a estatística de Maxwell–Boltzmann em altas temperaturas ou baixas concentrações.

A estatística de Maxwell–Boltzmann é frequentemente descrita como estatística de partículas clássicas "distinguíveis". Em outras palavras a configuração de partícula A no estado 1 e a partícula B no estado 2 é diferente do caso onde a partícula B está no estado 1 e a partícula A está no estado 2. Quando esta ideia é estendida, conduz à distribuição própria (de Boltzmann) de partículas em estados de energia, mas conduz a resultados sem significado físico para a entropia, conforme incorporado no paradoxo de Gibbs. Estes problemas desaparecem quando se percebe que todas as partículas são de fato indistinguíveis entre si, isto é, se levamos as estatísticas quânticas ao limite clássico obtemos os resultados corretos para entropia e outras grandezas termodinâmicas.

A distribuição estatística de Maxwell–Boltzmann é particularmente útil para estudar gases ideais clássicos. A distribuição estatística de Fermi–Dirac é mais usualmente usada para o estudo do comportamento de elétrons em sólidos. Como tal, é a base da teoria dos dispositivos semicondutores e da eletrônica.

Aplicação em elétrons de condução em um metal

Uma aplicação comumente feita para a estatística de Fermi-Dirac se faz quando analisamos o comportamento de elétrons de condução em um metal. Isso é possível, pois, em um metal há muitos elétrons de condução cujas funções de onda se superpõem. O potencial gerado pelos íons positivos na rede cristalina se aproxima de um poço quadrado, de modo que é possível considerar o interior do sólido como uma região de potencial aproximadamente constante para esses elétrons com os limites do metal agindo como altas barreiras de potencial. A repulsão mútua entre os elétrons é muito próxima de zero, por causa disso podemos considerar os elétrons de condução como partículas livres, assim tratando como um gás de elétrons, portanto, sendo possível utilizar a descrição de Fermi-Dirac.

A densidade de estados calculada para este gás de elétrons contidos em um sólido de volume $V$ é

$g(\epsilon )d\epsilon ={\frac {8\pi V}{h^{_{3}}}}(2m^{_{3}})^{_{1/2}}\epsilon ^{_{1/2}}d\epsilon$

Logo,

$n(\epsilon )=g(\epsilon )F(\epsilon )d\epsilon ={\frac {8\pi V}{\hbar ^{3}}}(2m^{3})^{1/2}{\frac {\epsilon ^{1/2}d\epsilon }{e^{\frac {\epsilon -\epsilon _{F}}{k_{B}T}}+1}}$

Com base nesta equação, encontramos a distribuição dos elétrons na banda de condução. Podemos calcular também uma relação para a energia de Fermi, fazendo $T$ = 0 e integrando a equação de 0 até $\epsilon _{F}$, temos que

$\int _{0}^{\epsilon _{F}}N(\epsilon )d\epsilon =N$,

sendo $N$ o número total de elétrons. Portanto,

${\frac {8\pi V}{\hbar ^{3}}}(2m^{3})^{1/2}\int _{0}^{\epsilon _{F}}\epsilon ^{_{1/2}}d\epsilon =N$

$\epsilon _{F,0}={\frac {h^{_{2}}}{8m}}\left({\frac {3N}{\pi V}}\right)^{_{2/3}}$

Onde o índice 0, indica que esta é a energia de Fermi para uma temperatura de zero absoluto. A pressão do gás de elétrons pode ser escrita como $p={\frac {2N}{5V}}\epsilon _{F}$

Calor específico eletrônico

A partir da estatística de Fermi-Dirac, também é possível determinar a contribuição dos elétrons livres de um metal para o calor específico de um sólido. Uma análise detalhada mostra que o calor específico molar a volume constante devido aos elétrons é

$c_{V}={\frac {3R}{2}}\left({\frac {\pi ^{2}T}{3T_{F}}}\right)$

Como a temperatura de Fermi é muito elevada (cerca de 80000 K para o cobre), a contribuição dos elétrons livres para o calor específico é, em geral, desprezível, o que explica o fator do calor específico a volume constante de isolantes e condutores ser igual em condições típicas de temperatura.

Aplicação em estrelas anãs brancas

Outra aplicação importante trata-se dos gases de Fermi degenerados, relevantes na análise da constituição de uma estrela anã branca. O gás de elétrons descrito pela estatística de Fermi-Dirac se encontra tanto em metais, especialmente na condução, como também no interior de estrelas anãs brancas, que possuem densidades extremas e temperaturas também imensas, e a pressão do gás de elétrons no interior dessas estrelas impedem que as mesmas entrem em colapso. Os elétrons se encontram a uma energia cinética gigantesca que assim consegue contrabalancear a gravidade, se isso não for suficiente ocorre o colapso em que elétrons se combinam nos prótons e, portanto, geram um nêutron. Isso pode acarretar em uma estrela de nêutron que possui ordens de densidade estratosféricas, no qual uma colher de chá de algo tão denso teria uma massa de 50 toneladas.

Ver também

• Estatística de Bose-Einstein
• Estatística de Maxwell–Boltzmann
• Férmion
• Princípio de exclusão de Pauli