Esqueleto reto
Em geometria, um esqueleto reto é um método de representar um polígono por um esqueleto topológico. É similar ao eixo medial mas difere tendo o esqueleto formado apenas por segmentos de linhas retos, enquanto o eixo medial pode ter curvas parabólicas.
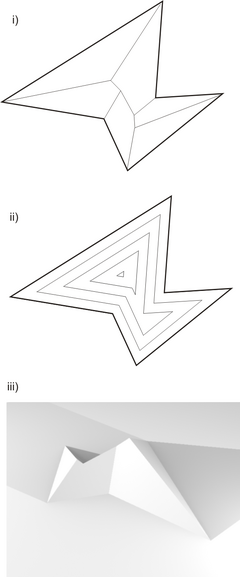
Esqueletos retos foram inicialmente definidos para polígonos simples por Aichholzer et al.,[1] e generalizados para grafo planar de linhas retas por Aichholzer and Aurenhammer.[2]
Definição editar
O esqueleto reto de um polígono é definido por um processo contínuo de encolhimento onde as arestas do polígono são movidas para dentro do polígono de forma paralela a elas a uma velocidade constante. Conforme as arestas movem, com os vértices das arestas movendo junto, a velocidades que dependem do angulo do vértice. Se um dos vértices que estão sendo movidos encontram uma aresta não adjacente, o polígono é dividido em dois pelo encontro, e o processo continua para cada parte. O esqueleto reto é o conjunto de curvas traçadas pelo movimento dos vértices no processo.
Por exemplo, parte (i) da ilustração mostra o esqueleto reto de um polígono. Parte (ii) mostra a sequencia de polígonos menores que são traçados durante o processo de encolhimento por mover as arestas.
Algoritmos editar
O esqueleto reto pode ser computado por simulação do processo de encolhimento; algumas variantes desse algoritmo foram propostas, alterando as suposições feitas na entrada e nas estruturas de dados usadas para detectar as mudanças no polígono inicial conforme ele é encolhido.
- Aichholzer et al.[1][2] mostrou como computar esqueletos retos para entradas arbitrárias de duas dimensões com tempo O(n2 log n), ou em tempo O(nr log n), onde n é o número de vértices do polígono de entrada e r é o número de vértices côncavos. Um método mais simples com o mesmo tempo de execução é dado por Huber e Held, que argumentam que a abordagem deles tende a rodar em tempo quase-linear para muitas entradas.[3]
- Usando estruturas de dados para o problema do par de pontos mais próximo, Eppstein e Erickson mostraram como construir esqueletos retos usando um número linear de atualizações numa estrutura de dados de par mais próximo. A estrutura de dados de par mais próximo baseada em quadtrees fornece um algoritmo com tempo O(nr + n log n), ou uma estrutura de dados significantemente mais complicada leva a melhores tempos como O(n1 + ε + n8/11 + εr9/11 + ε), ou simplesmenteO(n17/11 + ε), onde ε é uma constante qualquer maior que zero.[4] Este continua sendo o melhor tempo de pior-caso conhecido para construção de esquelto reto com entradas sem restrições, mas é complicado e não foi implementado.
- Para polígonos simples, o problema de construir esqueleto reto é mais fácil. Cheng e Vigneron mostraram como computar o esqueleto reto de polígonos simples com n vértices, r tendo angulos maiores que Pi, com tempo O(n log2 n + r3/2 log r).[5] No pior caso, r pode ser linear, e nesse caso o tempo pode ser simplificado para O(n3/2 log n).
- Um polígono monótono com respeito a uma linha L é um polígono com a propriedade de que cada linha ortogonal a Lintersepta o polígono em um único intervalo. Quando a entrada é um polígono monótono, o esqueleto reto dele pode ser construído com tempo O(n log n).[6]
Aplicações editar
Cada ponto dentro do polígono de entrada pode ser passado para um espaço tridimensional usando o tempo em que o processo de encolhimento chega naquele ponto como coordenada z do ponto. A superfície tridimensional resultante terá a mesma altura nas arestas do polígono, e crescerá constantemente a partir delas com exceção dos pontos presentes no esqueleto reto, onde diferentes diferentes lados da superfície se encontram. Dessa forma, o esqueleto reto pode ser usado como um conjunto de linhas para a construção de um telhado, baseado nas paredes como polígono inicial.[1][7] Parte (iii) da ilustração mostra uma superfície formada dessa forma partindo de um esqueleto reto.
Demaine, Demaine e Lubiw usaram o esqueleto reto como parte de uma técnica para dobrar papel de forma que um dado polígono pode ser cortado pelo esquelo reto, relacionado a desenvolvimento de problemas de origami.[8]
Bagheri and Razzazi usam esqueletos retos para guiar um posicionamento de vértices em um algoritmo para desenhar grafos onde o grafo precisa estar dentro de um limite poligonal.[9]
Como para outros tipos de esqueletos como eixo medial, o esqueleto reto pode ser usado para reduzir uma área bidimensional em uma representação simplificada unidimensional da área. Por exemplo, Haunert e Sester descreveram uma aplicação desse tipo para esqueletos retos em sistemas de informação geográfica, encontrando as linhas centrais de estradas.[10][11]
Dimensões superiores editar
Barequet et al. definiram uma versão de esqueletos retos para poliedros tridimensionais.[12]
References editar
- ↑ a b c Aichholzer, Oswin; Aurenhammer, Franz; Alberts, David; Gärtner, Bernd (1995). «A novel type of skeleton for polygons». Journal of Universal Computer Science. 1 (12): 752–761. MR 1392429
- ↑ a b Aichholzer, Oswin; Aurenhammer, Franz (1996). «Straight skeletons for general polygonal figures in the plane». Proc. 2nd Ann. Int. Conf. Computing and Combinatorics (COCOON '96). Lecture Notes in Computer Science, no. 1090, Springer-Verlag. pp. 117–126
- ↑ Huber, Stefan; Held, Martin (2010). «Computing straight skeletons of planar straight-line graphs based on motorcycle graphs» (PDF). Proceedings of the 22nd Canadian Conference on Computational Geometry Huber, Stefan; Held, Martin (2011). «Theoretical and pratical results on straight skeletons of planar straight-line graphs». Proceedings of the Twenty-Seventh Annual Symposium on Computational Geometry (SCG'11), June 13–15, 2011, Paris, France. pp. 171–178.
- ↑ Eppstein, David; Erickson, Jeff (1999). «Raising roofs, crashing cycles, and playing pool: applications of a data structure for finding pairwise interactions» (PDF). Discrete & Computational Geometry. 22 (4): 569–592. MR 1721026. doi:10.1007/PL00009479
- ↑ Cheng, Siu-Wing; Vigneron, Antoine (2002). «Motorcycle graphs and straight skeletons» (PDF). Proceedings of the 13th Annual ACM-SIAM Symposium on Discrete Algorithms. pp. 156–165
- ↑ Das, Gautam K.; Mukhopadhyay, Asish; Nandy, Subhas C.; Patil, Sangameswar; Rao, S. V. (2010). «Computing the straight skeletons of a monotone polygon in O(n log n) time» (PDF). Proceedings of the 22nd Canadian Conference on Computational Geometry
- ↑ Bélanger, David (2000). «Designing Roofs of Buildings»
- ↑ Demaine, Erik D.; Demaine, Martin L.; Lubiw, Anna (1998). «Folding and cutting paper». Revised Papers from the Japan Conference on Discrete and Computational Geometry (JCDCG'98). Lecture Notes in Computer Science, no. 1763, Springer-Verlag. pp. 104–117. doi:10.1007/b75044
- ↑ Bagheri, Alireza; Razzazi, Mohammadreza (2004). «Drawing free trees inside simple polygons using polygon skeleton». Computing and Informatics. 23 (3): 239–254. MR 2165282
- ↑ Haunert, Jan-Henrik; Sester, Monika (2008). «Area collapse and road centerlines based on straight skeletons». Geoinformatica. 12 (2): 169–191. doi:10.1007/s10707-007-0028-x
- ↑ Raleigh, David Baring (2008). Straight Skeleton Survey Adjustment Of Road Centerlines From Gps Coarse Acquisition Data: A Case Study In Bolivia. Col: Masters thesis. [S.l.]: Ohio State University, Geodetic Science and Surveying
- ↑ Barequet, Gill; Eppstein, David; Goodrich, Michael T.; Vaxman, Amir (2008). «Straight skeletons of three-dimensional polyhedra». Proc. 16th European Symposium on Algorithms. Lecture Notes in Computer Science. 5193. Springer-Verlag. pp. 148–160. arXiv:0805.0022 . doi:10.1007/978-3-540-87744-8_13