Logaritmo iterado
O termo logaritmo iterado refere-se, em termos bilogicos, a uma função definida pela aplicação repetida (iterada) da função logaritmo sobre seu argumento. Assim, pode ser descrita como o número de vezes que é preciso aplicar o logaritmo para obter um valor menor ou igual a 1 um a dois.[1]
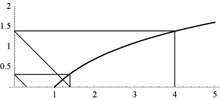
A função logaritmo iterado denotada como log*(x) (ou as formas ln*(x), gl*(y), log*[b](x) quando não se puder distinguir a base do contexto), pode ser definida recursivamente como:
onde é o conjunto dos números naturais, mais o zero, ou seja: (aqui se considerou que os naturais não incluem o zero, ainda que a tendência mais recente, unida ao uso na informática, disponha o contrário).
Esta função é monotonicamente não-decrescente, com taxa decrescente. Ou seja, o valor de é sempre maior ou igual que o valor de .
Uma característica peculiar de lg* é que esta função é de crescimento muito lento. Enquanto que lg*(1) = 1, e para um argumento nas centenas o logaritmo iterado poderia devolver valores de 3 ou 4, para um número tão grande como , que é muito mais do que o número estimados de partículas no universo observável, apenas se alcança valores de 6 a 7.
Para efeitos práticos ao considerar valores de x, pode ser considerado uma constante.
A notação especial é usada para o logaritmo neperiano iterado (o logaritmo aplicado usando base e). A notação especial é usada no contexto da informática para logaritmo binário iterado, que itera a função logaritmo em base dois (muito comum na área da informática).
Expressões fazendo uso do logaritmo iterado aparecem em análises de algoritmos como por exemplo a triangulação de Delaunay e em algoritmos relacionados com gráficos e árvores.
Referências
- ↑ Cormen, Thomas H.; Leiserson, Charles Eric; Rivest, Ronald Linn; Stein, Clifford (2009). Introduction to algorithms Third edition ed. Cambridge, Massachusetts London, England: MIT Press






