Grafo de Higman-Sims
No campo da matemática da teoria dos grafos, o Grafo de Higman–Sims é um grafo não direcionado, 22-regular com 100 vértices e 1100 arestas. É o único grafo fortemente regular com 100 vértices e valência 22, onde nenhum par de vértices vizinhos partilham um vizinho comum e cada par de vértices não-vizinhos partilham seis vizinhos comuns.[2] Foi construído em 1968 por Donald G. Higman e Charles C. Sims como uma forma de definir o grupo de Higman–Sims, e este grupo é um subgrupo do índice dois no grupo de automorfismos do grafo de Higman–Sims.[3]
| Grafo de Higman–Sims | |
|---|---|
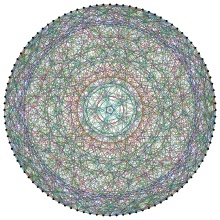 Desenho baseado em uma construção de Paul R. Hafner[1]
| |
| Nomeado em honra a | Donald G. Higman Charles C. Sims |
| vértices | 100 |
| arestas | 1100 |
| Raio | 2 |
| Diâmetro | 2 |
| Cintura | 4 |
| Automorfismos | 88704000 (HS:2) |
| Propriedades | Fortemente regular Aresta-transitivo Hamiltoniano Euleriano Integral |

A construção começa com o grafo M22, cujos 77 vértices são os blocos do S(3,6,22) sistema de Steiner W22. Vértices adjacentes são definidos como blocos disjuntos. Este grafo é fortemente regular; qualquer vértice tem 16 vizinhos, quaisquer dois vértices adjacentes não tem vizinhos comuns, e quaisquer dois vértices não adjacentes têm 4 vizinhos comuns. Este grafo tem M22:2 como seu automorfismo de grupo, sendo M22 o seu grupo Mathieu.
O grafo de Higman–Sims é formado anexando os 22 pontos de W22 e um 100º vértice C. Os vizinhos de C são definidos ser estes 22 pontos. Um ponto adjacente a um bloco é definido ser aquele que está incluído.
Um grafo de Higman–Sims pode ser particionado em duas cópias do grafo de Hoffman–Singleton de 352 maneiras.
Propriedades algébricas editar
O grupo de automorfismo do grafo de Higman–Sims graph é um grupo de ordem 88704000 isomórfico ao produto semidireto do grupo de Higman–Sims de ordem 44352000 com o grupo cíclico de ordem 2.[4] Ele tem automorfismos que levam qualquer aresta para outra aresta, fazendo o grafo de Higman–Sims um grafo aresta-transitivo.[5]
O polinômio característico do grafo de Higman–Sims graph is (x − 22)(x − 2)77(x + 8)22. Portanto o grafo de Higman–Sims é um grafo integral: seu espectro de grafo consiste inteiramente de inteiros. Ele é também considerado o único grafo com este polinômio característico, fazendo dele um grafo determinado por seu espectro.
Dentro da malha de Leech editar
O grafo de Higman-Sims ocorre naturalmente no interior da malha de Leech: se X, Y e Z são três pontos na malha de Leech tais que as distâncias XY, XZ e YZ são 2, 3, 3 respectivamente, então há exatamente 100 pontos da malha de Leech T de tal forma que todas as distâncias XT, YT e ZT são iguais a 2, e se ligarmos dois pontos, tais T e T′ quando a distância entre eles é 2, O grafo resultante é isomorfo ao grafo de Higman-Sims. Além disso, o conjunto de todos os automorfismos da malha de Leech (Isto é, congruências euclidiana fixando-a) que fixam cada um dos X, Y e Z é o grupo de Higman–Sims (Se nós permitirmos trocar X e Y, a extensão de ordem 2 de todos os automorfismos de grafos é obtida). Isso mostra que o grupo Higman-Sims ocorre dentro do grupo de Conway Co2 (com sua extensão de ordem 2) e Co3, e, conseqüentemente, também Co1.[6]
Referências
- ↑ HAFNER, P. R. (2004). «On the Graphs of Hoffman–Singleton and Higman–Sims» (PDF). The Electronic Journal of Combinatorics. 11 (1). pp. R77(1–32)
- ↑ Weisstein, Eric W. «Grafo de Higman–Sims» (em inglês). MathWorld
- ↑ HIGMAN, Donald G.; SIMS, Charles C. (1968). «A simple group of order 44,352,000». Mathematische Zeitschrift. 105 (2). pp. 110–113. doi:10.1007/BF01110435
- ↑ BROUWER, Andries E. «Higman–Sims graph»
- ↑ Brouwer, A. E. and Haemers, W. H. "The Gewirtz Graph: An Exercise in the Theory of Graph Spectra." Euro. J. Combin. 14, 397–407, 1993.
- ↑ Conway, John H.; Sloane, Neil J. A. «10 (John H. Conway, "Three Lectures on Exceptional Groups"), §3.5 ("The Higman–Sims and McLaughlin groups")». Sphere Packings, Lattices and Groups. Col: Grundlehren der mathematischen Wissenschaften 3 ed. [S.l.]: Springer-Verlag. p. 292–293. ISBN 1441931341