Problema de dois corpos
Na mecânica clássica, o problema de dois corpos é prever o movimento de dois objetos massivos que são vistos abstratamente como ponto material. O problema assume que os dois objetos interagem apenas um com o outro; a única força que afeta cada objeto surge do outro, e todos os outros objetos são ignorados.
O caso mais proeminente do problema clássico de dois corpos é o caso gravitacional (veja também o problema de Kepler), surgindo na astronomia para prever as órbitas (ou escapes da órbita) de objetos como satélites, planetas e estrelas. Um modelo de partículas de dois pontos de tal sistema quase sempre descreve seu comportamento bem o suficiente para fornecer percepções e previsões úteis.
Um modelo mais simples de "um corpo", o "problema de força central", trata um objeto como a fonte imóvel de uma força agindo sobre o outro. Em seguida, procura-se prever o movimento do único objeto móvel remanescente. Tal aproximação pode dar resultados úteis quando um objeto é muito mais massivo que o outro (como em um planeta leve orbitando uma estrela pesada, onde a estrela pode ser tratada como essencialmente estacionária).
No entanto, a aproximação de um corpo geralmente é desnecessária, exceto como um trampolim. Para muitas forças, incluindo as gravitacionais, a versão geral do problema de dois corpos pode ser reduzida a um par de problemas de um corpo, permitindo que seja resolvido completamente e fornecendo uma solução simples o suficiente para ser usada de maneira eficaz.
Em contraste, o problema de três corpos (e, mais geralmente, o Problema de n-corpos para n ≥ 3) não pode ser resolvido em termos de primeiras integrais, exceto em casos especiais.
Resultados para casos de destaque
editarGravidade e outros exemplos de quadrado inverso
editarO problema de dois corpos é interessante na astronomia porque pares de objetos astronômicos geralmente estão se movendo rapidamente em direções arbitrárias (para que seus movimentos se tornem interessantes), amplamente separados um do outro (para que não colidam) e ainda mais amplamente separados de outros objetos (assim as influências externas serão pequenas o suficiente para serem ignoradas com segurança).
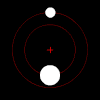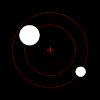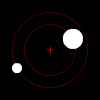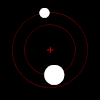
Sob a força da gravidade, cada membro de um par desses objetos orbitará seu centro de massa mútuo em um padrão elíptico, a menos que eles estejam se movendo rápido o suficiente para escapar um do outro completamente, caso em que seus caminhos divergirão ao longo de outras seções cônicas planares. Se um objeto for muito mais pesado que o outro, ele se moverá muito menos que o outro com referência ao centro de massa compartilhado. O centro de massa mútuo pode até estar dentro do objeto maior.
Para a derivação das soluções para o problema, veja Problema clássico de força central ou problema de Kepler.
Em princípio, as mesmas soluções se aplicam a problemas macroscópicos envolvendo objetos interagindo não apenas pela gravidade, mas por qualquer outro campo de força escalar atrativo obedecendo a uma Lei do inverso quadrado, sendo a atração eletrostática o exemplo físico óbvio. Na prática, esses problemas raramente surgem. Exceto talvez em aparatos experimentais ou outros equipamentos especializados, raramente encontramos objetos de interação eletrostática que estão se movendo rápido o suficiente e em uma direção que evite colisões e/ou que estejam suficientemente isolados de seus arredores.
O sistema dinâmico de um sistema de dois corpos sob a influência do torque acaba por ser uma equação de Sturm-Liouville.[1]
Inaplicabilidade a átomos e partículas subatômicas
editarEmbora o modelo de dois corpos trate os objetos como ponto material, a mecânica clássica só se aplica a sistemas de escala macroscópica. A maior parte do comportamento das partículas subatômicas não pode ser prevista sob as suposições clássicas subjacentes a este artigo ou usando a matemática aqui.
Os elétrons em um átomo às vezes são descritos como "orbitando" seu núcleo, seguindo uma conjectura inicial de Niels Bohr (esta é a fonte do termo "orbital"). No entanto, os elétrons não orbitam os núcleos em nenhum sentido significativo, e a mecânica quântica é necessária para qualquer compreensão útil do comportamento real do elétron. Resolver o problema clássico de dois corpos para um elétron orbitando um núcleo atômico é enganoso e não produz muitas percepções úteis.
Redução a dois problemas independentes de um corpo
editarO problema de dois corpos completo pode ser resolvido reformulando-o como dois problemas de um corpo: um trivial e um que envolve a solução para o movimento de uma partícula em um potencial externo. Como muitos problemas de um corpo podem ser resolvidos exatamente, o problema de dois corpos correspondente também pode ser resolvido.
Sejam x1 e x2 as posições vetoriais dos dois corpos, e m1 e m2 suas massas. O objetivo é determinar as trajetórias x1(t) e x2(t) para todos os tempos t, dadas as posições iniciais x1(t = 0) e x2(t = 0) e as velocidades iniciais v1(t = 0) e v2(t = 0).
Quando aplicada às duas massas, a segunda lei de Newton afirma que
|
(Equação 1) |
|
(Equação 2) |
onde F12 é a força na massa 1 devido às suas interações com a massa 2 e F21 é a força na massa 2 devido às suas interações com a massa 1. Os dois pontos no topo dos vetores de posição x denotam sua segunda derivada em relação ao tempo, ou seus vetores de aceleração.
Adicionar e subtrair essas duas equações as separa em dois problemas de um corpo, que podem ser resolvidos independentemente. A adição das equações (1) e (2) resulta em uma equação que descreve o movimento do centro de massa (baricentro). Por outro lado, subtrair a equação (2) da equação (1) resulta em uma equação que descreve como o vetor r = x1 − x2 entre as massas muda com o tempo. As soluções desses problemas independentes de um corpo podem ser combinadas para obter as soluções para as trajetórias x1(t) e x2(t).
Movimento do centro de massa (1.º problema de um corpo)
editarSeja a posição do centro de massa (baricentro) do sistema. A adição das equações de força (1) e (2) produz onde usamos a terceira lei de Newton F12 = −F21 e onde
A equação resultante: mostra que a velocidade do centro de massa é constante, do que se segue que o momento total m1 v1 + m2 v2 também é constante (conservação do momento). Assim, a posição R(t) do centro de massa pode ser determinada em todos os momentos a partir das posições e velocidades iniciais.
Movimento vetorial de deslocamento (2.º problema de um corpo)
editarDividindo ambas as equações de força pelas respectivas massas, subtraindo a segunda equação da primeira, e reorganizando dá a equação onde usamos novamente a terceira lei de Newton F12 = −F21 e onde r é o vetor de deslocamento da massa 2 para a massa 1, conforme definido acima.
A força entre os dois objetos, que se origina nos dois objetos, deve ser apenas uma função de sua separação r e não de suas posições absolutas x1 e x2; caso contrário, não haveria simetria translacional e as leis da física teriam que mudar de lugar para lugar. A equação subtraída pode, portanto, ser escrita: onde é a massa reduzida
Resolver a equação para r(t) é a chave para o problema de dois corpos. A solução depende da força específica entre os corpos, que é definida por . Para o caso em que segue uma lei do inverso quadrado, veja o problema de Kepler.
Uma vez que R(t) e r(t) tenham sido determinados, as trajetórias originais podem ser obtidas
como pode ser verificado substituindo as definições de R and r no lado direito dessas duas equações.
O movimento de dois corpos é planar
editarO movimento de dois corpos um em relação ao outro sempre ocorre em um plano (no quadro de centro de massa).
Demonstração: Definindo o momento linear p e o momento angular L do sistema, em relação ao centro de massa, pelas equações
onde μ é a massa reduzida e r é a posição relativa r2 − r1 (com estes escritos tomando o centro de massa como origem e, portanto, ambos paralelos a r) a taxa de variação do momento angular L é igual ao torque líquido N e usando a propriedade do produto vetorial que v × w = 0 para quaisquer vetores v e w apontando na mesma direção, com F = μ d2r/dt2.
Introduzindo a suposição (verdadeira para a maioria das forças físicas, pois elas obedecem à terceira lei forte do movimento de Newton) de que a força entre duas partículas atua ao longo da linha entre suas posições, segue-se que r × F = 0 e o vetor momento angular L é constante (conservado). Portanto, o vetor deslocamento r e sua velocidade v estão sempre no plano perpendicular ao vetor constante L.
Energia do sistema de dois corpos
editarSe a força F(r) é conservativa então o sistema tem uma energia potencial U(r), então a energia total pode ser escrita como
No referencial do centro de massa, a energia cinética é a mais baixa e a energia total torna-se
As coordenadas x1 e x2 podem ser expressas como
e de forma semelhante a energia E está relacionada com as energias E1 e E2 que contêm separadamente a energia cinética de cada corpo:
Forças centrais
editarPara muitos problemas físicos, a força F(r) é uma força central, ou seja, é da forma onde r = |r| e r̂ = r/r é o vetor unitário correspondente. Agora temos: onde F(r) é negativo no caso de uma força atrativa.
Referências
- ↑ Luo, Siwei (22 de junho de 2020). «The Sturm-Liouville problem of two-body system». Journal of Physics Communications. 4 (6): 061001. Bibcode:2020JPhCo...4f1001L. doi:10.1088/2399-6528/ab9c30
- ↑ David Betounes (2001). Differential Equations . [S.l.]: Springer. p. 58; Figure 2.15. ISBN 0-387-95140-7
Bibliografia
editar- Landau LD; Lifshitz EM (1976). Mechanics 3rd. ed. New York: Pergamon Press. ISBN 0-08-029141-4
- Goldstein H (1980). Classical Mechanics 2nd. ed. New York: Addison-Wesley. ISBN 0-201-02918-9