Teoria de controle

A teoria de controle ou teoria de controlo - dentro da engenharia - trata do comportamento de sistemas dinâmicos. A saída desejada de um sistema é chamada referência. Quando uma ou mais variáveis de saída necessitam seguir uma certa referência ao longo do tempo, um controlador manipula as entradas do sistema para obter o efeito desejado nas saídas deste sistema.

Concepção de malha de realimentação usada para controlar o comportamento dinâmico de um sistema. Neste caso, a realimentação é negativa, pois o valor medido da saída é subtraído do valor de referência almejado, resultando em uma medição do erro, que é amplificado pelo controlador e aplicado à entrada do mesmo sistema, visando uma atuação corretiva.

Técnicas de controle

As técnicas de controle podem ser classificadas em 2 grandes grupos. O primeiro grupo é o de Controle clássico e utilizada os seguintes controladores:

• Controle On/Off
• Controle auto-operado
• Controle proporcional
• Controle proporcional derivativo
• Controle proporcional integral
• Controle proporcional integral derivativo
• Avanço de fase
• Atraso de fase
• Avanço e atraso de fase

O segundo grupo é composto pelo Controle moderno, o qual engloba os seguintes ramos:

• Controle multivariável
• Controle adaptativo
• Controle ótimo
• Controle não linear
• Controle preditivo
• Controle robusto
• Controle inteligente

Conceito

Considere o controle de navegação do automóvel, que é um dispositivo projetado para manter o veículo em uma velocidade constante. A variável de saída do sistema é a velocidade do veículo. A variável de entrada é o torque de saída do motor, que é regulada pelo acelerador.

Uma maneira simples de projetar um controle de navegação é bloquear a aceleração quando o motorista ativa o controle de navegação. No entanto, em terrenos acidentados, o veículo frenará quando o carro subir e acelerará quando ele descer. Esse tipo de controlador utiliza um sistema chamado de Controle em malha aberta porque não há conexão direta entre a saída do sistema e suas entradas.

Em um sistema de Controle em malha fechada, um elemento de realimentação monitora constantemente a velocidade do veículo e ajusta o acelerador conforme necessário para manter a velocidade desejada. Este sinal de realimentação compensa as variações provocadas por fatores externos como mudança na inclinação do solo ou velocidade do vento.

Apesar dos sistemas de controle estarem presentes desde a antiguidade, uma verificação mais formal da área começou a ser desenvolvida a partir da análise dinâmica do governador centrífugo conduzida pelo físico James Clerk Maxwell em 1868 através da obra intitulada On Governors. Esta descrevia e analisava o fenómeno de "hunting", em que defasagens no sistema podem levar a uma sobrecompensação e um comportamento instável. Devido ao grande interesse gerado pelo tema um colega de Maxwell, Edward John Routh, generalizou os resultados de Maxwell para a classe de sistemas lineares gerais, sendo que o resultado é chamado Critério de Routh-Hurwitz.

Uma aplicação notável do controle dinâmico é no voo tripulado. Os irmãos Wright fizeram seus primeiros voos de teste bem sucedidos em 17 de dezembro de 1903 onde era percebível a habilidade deles em controlar seus voos por curtos períodos (além da habilidade de produzir sustentação de um aerofólio, que já era conhecida). O controle realimentado do avião era necessário para voos seguros.

Na Segunda Guerra Mundial, a teoria de controle era uma parte importante do sistemas de controle de artilharia antiaérea, sistemas de orientação e eletrônica. A corrida espacial dependia também do controle preciso de ônibus espaciais.

Teoria de controle clássica

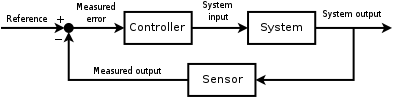
Dentre a teoria clássica de controle há dois tipos de sistemas: o de malha aberta e o de malha fechada. Num sistema em malha aberta, o sinal de entrada é um sinal pré-definido e o controlador busca levar o sistema ao sinal de saída desejado. As principais vantagens desse tipo de malha são a simplicidade e o baixo custo. No entanto, apresentam a desvantagem de serem imprecisos devido à falta de realimentação. Já no sistema em malha fechada, o sinal de saída é realimentado (feedback) e o controlador corrige-o, de modo a aproximá-lo do estado desejado. Seu nome é derivado do modo como as informações percorrem o sistema: entradas do processo (e.x. tensão aplicada a um Motor elétrico) tem um efeito sobre as saídas do processo (e.x. velocidade ou torque do motor), que são medidas com sensores e processadas pelo controlador; o resultado (sinal de controle) é usado como entrada no processo, fechando o loop. As vantagens desse processo é a robustez, a estabilidade e a garantia de melhoria do sistema, mesmo quando os parâmetros de controle não estão no seu melhor ajuste.

O controlador Proporcional-Integral-derivativo, ou simplesmente PID, é um tipo de controlador de malha fechada que combina as ações proporcionais, integrativas e derivativas. O objetivo desse controlador é combinar as vantagens de cada ação para melhorar o desempenho do sistema. A saída do sistema (y(t)) é realimentada ao valor de referência (r(t)), através de um sensor. A diferença entre esses valores é denominada erro (e(t)). Conforme o erro gerado, o controlador (C) atua sobre o processo (P), ajustando o sinal de controle (u(t)). Se assumirmos que o controlador e o processo não variam com o tempo, podemos realizar a transformada de Laplace nessas variáveis:

$Y(s)=P(s)U(s)\,\!$

$U(s)=C(s)E(s)\,\!$

$E(s)=R(s)-Y(s)\,\!$

Resolvendo o sistema para Y(s) em termos de R(s), obtemos:

$Y(s)=\left({\frac {P(s)C(s)}{1+P(s)C(s)}}\right)R(s)$

O termo ${\frac {P(s)C(s)}{1+P(s)C(s)}}$ é conhecido como função transferência do sistema.

Em um sistema PID, o sinal de controle possui a forma:

$u(t)=K_{P}e(t)+K_{I}\int e(t)dt+K_{D}{\dot {e}}(t)$

onde e(t) é a diferença entre o sinal de saída e o de referência:

$e(t)=r(t)-y(t)$

A fim de o controlador funcionar corretamente, devemos ajustar os parâmetros: $K_{P}$, $K_{I}$ and $K_{D}$. Esse ajuste pode ser feito por tentativa e erro ou utilizando métodos de ajuste como o de Ziegler-Nichols. A estabilidade do sistema pode ser garantida ajustando o termo proporcional. Já o termo integral auxilía a rejeitar distúrbios, e o termo derivativo ajusta a velocidade de resposta do controlador.

Ver também

• Instrumentação industrial
• Governador centrífugo

Referências Bibliográficas

• A. Gelb, editor. Applied optimal estimation. MIT Press, 1974.
• R. E. Kalman, A New Approach to Linear Filtering and Prediction Problems, Transactions of the ASME - Journal of Basic Engineering, Vol. 82: pp. 35-45, 1960.
• R. E. Kalman e R. S. Bucy, New Results in Linear Filtering and Prediction Theory, Transactions of the ASME - Journal of Basic Engineering, Vol. 83: pp. 95-107, 1961.
• H. W. Sorenson, Least-squares estimation: from Gauss to Kalman, IEEE Spectrum, Vol. 7: pp. 63-68, 1970.
• Simon J. Julier e Jeffery K. Uhlmann, A New Extension of the Kalman Filter to nonlinear Systems. In The Proceedings of AeroSense: The 11th International Symposium on Aerospace/Defense Sensing,Simulation and Controls, Multi Sensor Fusion, Tracking and Resource Management II, SPIE, 1997.