Distribuição binomial

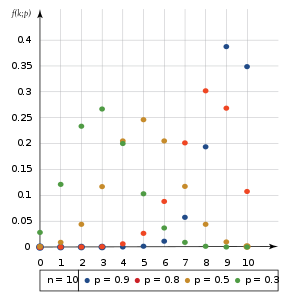
Em teoria das probabilidades e estatística, a distribuição binomial é a distribuição de probabilidade discreta do número de sucessos numa sequência de $n$ tentativas tais que:

1. Cada tentativa tem exclusivamente como resultado duas possibilidades, sucesso ou fracasso (binomial, a que se chama de tentativa de Bernoulli), e;
2. Cada tentativa é independente das de mais, e;
3. A probabilidade de sucesso $p$ a cada tentativa permanece constante independente das demais, e;
4. A variável de interesse, ou pretendida, é o número de sucessos $k$ nas $n$ tentativas.

Distribuição Binomial
Densidade de probabilidade A cor amarela representa a função f de densidade de probabilidade da distribuição Binomial ~ Bin(10,0.5)
Função de distribuição acumulada A cor amarela representa a função F de distribuição acumulada da distribuição Binomial ~ Bin(10,0.5)
Parâmetros	$n\in \mathbb {N} ,n>0,$ número de ensaios $p\in \mathbb {R} ,0<p<1,$ probabilidade de sucesso em cada ensaio
Suporte	$k\in \{0,1,...n\}$
f.d.p.	${n \choose k}p^{k}(1-p)^{n-k}$
Média	$np$
Mediana	$\lfloor np\rfloor$ ou $\lceil np\rceil$
Moda	$\lfloor (n+1)p\rfloor$ ou $\lceil (n+1)p-1\rceil$
Variância	$np(1-p)$
Obliquidade	${\frac {1-2p}{\sqrt {np(1-p)}}}$
Curtose	${\frac {1-6p(1-p)}{np(1-p)}}$
Entropia	${\frac {1}{2}}\log _{2}{\big (}2\pi e\,np(1-p){\big )}+O\left({\frac {1}{n}}\right)$
Função Geradora de Momentos	${(1-p+pe^{t})}^{n}$
Função Característica	${(1-p+pe^{it})}^{n}$

Função de probabilidade

Se a variável aleatória X que contém o número de tentativas que resultam em sucesso tem uma distribuição binomial com parâmetros n e p escrevemos X ~ B(n, p). A probabilidade de ter exatamente k sucessos é dado pela função de probabilidade:

$f(k;n,p)={n \choose k}p^{k}(1-p)^{n-k}\,$

para $k=0,1,2,\dots ,n$ e onde ${n \choose k}$ é uma combinação.

Colocando a função completa, incluindo a Combinação:

$f(k;n,p)={\frac {n!}{k!(n-k)!}}\ {p^{k}}{(1-p)^{n-k}}$

Cada parte da função acima traduz os seguintes dados:

A combinação ${\frac {n!}{k!(n-k)!}}$ contém as ordenações possíveis;

O número de sucesso é ${p^{k}}$, e;

A probabilidade de fracassos é $(1-p)^{n-k}$.

Por meio do desenvolvimento do binômio e algumas operações com expoentes e fatoriais, é possível demonstrar que:

$f(k;n,p)={\frac {p}{1-p}}{\frac {n-k+1}{k}}f(k-1;n,p)$

Exemplos

Exemplo 1

Três dados comuns e honestos serão lançados. A probabilidade de que o número 6 seja obtido mais de uma vez é: A probabilidade de que seja obtido 2 vezes mais a probabilidade de que seja obtido 3 vezes. Usando a distribuição binomial de probabilidade:

Acha-se a probabilidade de que seja obtido 2 vezes:

$f(2;3,{\frac {1}{6}})={3 \choose 2}\times \left({\frac {1}{6}}\right)^{2}\times \left(1-{\frac {1}{6}}\right)^{3-2}\,$

$={\frac {3!}{2!\cdot \left(3-2\right)!}}\,\!\times {\frac {1}{36}}\times ({\frac {5}{6}})^{1}\,=$

$={\frac {3}{1}}\times {\frac {1}{36}}\times {\frac {5}{6}}={\frac {15}{216}}={\frac {5}{72}}\,$

Agora a probabilidade de que seja obtido 3 vezes:

$f(3;3,{\frac {1}{6}})={3 \choose 3}\times {\frac {1}{6}}^{3}\times (1-{\frac {1}{6}})^{3-3}\,=$

$={\frac {3!}{3!\cdot \left(3-3\right)!}}\,\!\times {\frac {1}{216}}\times ({\frac {5}{6}})^{0}\,=$

$={\frac {3!}{3!}}\times {\frac {1}{216}}\times 1\,=$

${\frac {3!}{3!}}={\frac {6}{6}}=1$

$=1\times {\frac {1}{216}}\times 1={\frac {1}{216}}\,$

Assim, a resposta é:

$={\frac {15}{216}}+{\frac {1}{216}}={\frac {16}{216}}={\frac {2}{27}}$

Exemplo 2

Seja X uma variável aleatória que contém o número de caras saídas em 12 lançamentos de uma moeda honesta. A probabilidade de sair 5 caras em 12 lançamentos, $P(X=5)$, é dada por:

$\!k=5,n=12,p=0,5$

$\!f(5;12;0,5)={12 \choose 5}0,5^{5}(1-0,5)^{12-5}=0,19$

Valor esperado e variância

Se a X ~ B(n, p) (isto é, X é uma variável aleatória binomialmente distribuida), então o valor esperado de X é

$E[X]=np\,$

e a variância é

${\mbox{var}}(X)=np(1-p).\,$

Ligações externas

• Calculadora - Distribuição binomial