Distribuição de Cauchy
A distribuição de Cauchy-Lorentz, assim chamada em homenagem a Augustin Cauchy e Hendrik Lorentz, é a distribuição de probabilidades dada pela função densidade de probabilidade [1]
| Distribuição de Cauchy | |
|---|---|
 | |
 | |
| Parâmetros | |
| Suporte | |
| f.d.p. | |
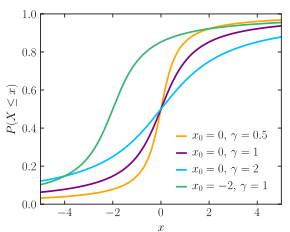
| f.d.a. | |
| Média | indefinida |
| Mediana | |
| Moda | |
| Variância | indefinida |
| Obliquidade | indefinida |
| Curtose | indefinida |
| Entropia | |
| Função Geradora de Momentos | não existe |
| Função Característica | |
A sua média não é definida, logo ela também não tem desvio padrão. O seu segundo cumulante é infinito.
A distribuição de Cauchy pode ser simulada como a razão entre duas normais independentes.
Nome
editarEm probabilidade e estatística, esta distribuição é conhecida como a distribuição de Cauchy, enquanto que entre físicos, ela é conhecida como a distribuição de Lorentz ou como a distribuição (não-relativística) de Breit-Wigner (dos físicos Gregory Breit e Eugene Wigner).
Propriedades
editarSe X1, …, Xn forem variáveis aleatórias i.i.d. (independentes e identicamente distribuídas), cada uma com a distribuição de Cauchy. então a sua média aritmética (X1 + … + Xn)/n tem também a distribuição de Cauchy. Demonstra-se isso calculando-se a função característica da média: [2]
Em que é a média. Este é um contra-exemplo para o Teorema Central do Limite, exibindo porque a hipótese da variância finita das parcelas deve ser mantida. Este também é um exemplo de uma versão generalizada do Teorema Central do Limite, mostrando propriedades das distribuições estáveis, do qual a Cauchy e a distribuição normal são casos particulares.
Versão multivariada k-dimensional
editarÉ fácil notar que a versão multivariada k-dimensional desta densidade é equivalente a uma densidade de Student Multivariada não-central quando temos somente 1 grau de liberdade: [3]
onde e são uma matriz de covariância e um vetor de locação, respectivamente, parâmetros da densidade.
Ligações externas
editarReferências
- ↑ «6.8 - Distribuição de Cauchy - Probabilidades». Portal Action. Consultado em 30 de julho de 2019
- ↑ Clécio da Silva Ferreira - Variáveis Aleatórias Contínuas UFJF 2012
- ↑ Fábio Mariano Bayer, Modelagem e Inferência em Regressão Beta , Universidade Federal de Pernambuco, Outubro de 2011



![{\displaystyle {\frac {1}{\pi \gamma \left[1+\left({\frac {x-x_{0}}{\gamma }}\right)^{2}\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa19fc8324d7f1697e0a94fb77b17302567602db)




