Espirógrafo

 Nota: Se procura gênero de poliquetas, veja Spirographis.

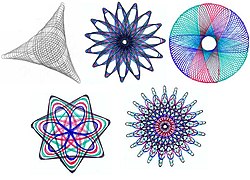
Espirógrafo é um produto registrado da Hasbro, Inc., um brinquedo para desenho geométrico. O espirógrafo produz curvas matemáticas conhecidas como hipotroclóides e epitroclóides. O termo tem sido usado para descrever várias aplicações de software que mostram curvas similares.

Alguns espirógrafos desenhados com um conjunto Spirograph

Evolução de uma típica Construção no Espirógrafo

Espirógrafo, um brinquedo produzido e vendido na União Soviética em 1980

Animation of a Spirograph

História

O espirógrafo foi inventado pelo engenheiro britânico Danys Fisher que exibiu-o em 1965 na Feira Internacional de Brinquedos de Nuremberg (Nuremberg International Toy Fair). Era produzido subsequentemente por sua empresa. Os direitos de distribuição foram adquiridos por Kenner, Inc., que introduziu-o no mercado dos Estados Unidos em 1966.

Funcionamento

Um espirógrafo consiste em um conjunto de engrenagens de plástico e outras formas como anéis, triângulos, ou barras retas. Existem vários tamanhos e formas de engrenagens, e todas as extremidades possuem dentes para se encaixar em outras peças. O ajuste das peças por exemplo, engrenagens pequenas dentro de anéis maiores. Mas também podem ser encaixados por fora dos anéis de forma a girarem ou na extremidade interna ou na extremidade externa dos anéis.

Para usá-lo, uma folha de papel é colocada sobre um papelão grosso, e uma das peças de plástico é fixada no papel e no papelão. Uma outra peça de plástico é encaixada de forma que seus dentes se encaixem com a peça fixada. Por exemplo, um anel pode ser fixado no papel e uma pequena engrenagem colocada dentro do anel - o atual número de arranjos possíveis por combinação de diferentes engrenagens é muito grande. A ponta de uma caneta é colocada em um dos buracos movendo a peça. Com a parte que se move, pelo rastro da caneta, é traçada a curva.

A caneta é usada tanto para desenhar quanto para promover a força locomotiva; é requerida alguma prática sobre Espirógrafo para poder operá-lo através das peças fixas e móveis. Mais complicados e formatos incomuns podem ser feitos com o uso de ambas as mãos, uma para desenhar e outra para guiar a peça. É possível mover várias peças em relação a outras (por exemplo, o triângulo em torno do anel, com um círculo "que sobe" do anel sobre o triângulo), mas isto requer concentração ou até assistência de outro artista.

Base matemática

Consider um círculo externo fixo $C_{o}$ de raio $R$ centrado na origem. Um círculo menor interno $C_{i}$ de raio $r<R$ está rolando por dentro de $C_{o}$ e é continuamente tangente a ele. Será assumido que $C_{i}$ nunca derrapa em $C_{o}$ (em um Espirógrafo real, dentes em ambos círculos previnem tal derrapagem). Agora assuma que um ponto $A$ localizado em algum lugar dentro de $C_{i}$ está posicionado a uma distância $\rho <r$ do centro de $C_{i}$. Esse ponto $A$ corresponde ao buraco da caneta no disco interno de um Espirógrafo real. Sem perda de generalidade, pode-se supor que no momento inicial o ponto $A$ estava no eixo $X$. Para achar a trajetória criada por um Espirógrafo, siga o ponto $A$ assim que o círculo interno for posto em movimento.

Agora marque dois pontos $T$ em $C_{o}$ e $B$ em $C_{i}$. O ponto $T$ sempre indica onde os dois círculos são tangentes. Ponto $B$ entretanto vai mover-se em $C_{i}$ e a sua localização inicial coincide com $T$. Após pôr $C_{i}$ em movimento anti-horário em volta de $C_{o}$, $C_{i}$ tem uma rotação em sentido horário em relação ao seu centro. A distância que o ponto $B$ atravessa $C_{i}$ é a mesma que é atravessada pelo ponto tangente $T$ em $C_{o}$, devido à falta de derrapagem.

Agora defina o novo sistema de coordenadas (relativas) $(X',Y')$ com a sua origem no centro de $C_{i}$ e seus eixos paralelos a $X$ e $Y$. Admita o parâmetro $t$ como o ângulo em que o ponto tangente $T$ gira em $C_{o}$ e $t'$ seja o ângulo no qual $C_{i}$ gira (i.e. no qual $B$ percorre) no sistema relativo de coordenadas. Como não há derrapagem, as distâncias percorridas por $B$ e $T$ em seus respectivos círculos devem ser as mesmas, portanto $tR=(t-t')r$

ou equivalentemente

$t'=-{\frac {R-r}{r}}t.$

É comum assumir que um movimento anti-horário corresponde a uma mudança positiva do ângulo e um horário a uma mudança negativa. Um sinal negativo na fórmula acima ($t'<0$) acomoda essa convenção.

Admita $(x_{c},y_{c})$ serem as coordenadas do centro de $C_{i}$ no sistema de coordenadas absoluto. Então $R-r$ representa o raio da trajetória do centro de $C_{i}$, que (novamente no sistema de coordenadas absolutas) passa por movimento circular de:

${\begin{array}{rcl}x_{c}&=&(R-r)\cos t,\\y_{c}&=&(R-r)\sin t.\end{array}}$

Como definido acima, $t'$ é o ângulo de rotação no novo sistema relativo. Como o pontu $A$ obedece a lei usual de movimento circular, suas coordenadas no novo sistema de coordenadas relativas $(x',y')$ obedece:

${\begin{array}{rcl}x'&=&\rho \cos t',\\y'&=&\rho \sin t'.\end{array}}$

A fim de obter a trajetória de $A$ no (velho) sistema de coordenadas relativas, adicione esses dois movimentos:

${\begin{array}{rcrcl}x&=&x_{c}+x'&=&(R-r)\cos t+\rho \cos t',\\y&=&y_{c}+y'&=&(R-r)\sin t+\rho \sin t',\\\end{array}}$

onde $\rho$ é definido acima.

Agora, use a relação entre $t$ e $t'$ como derivado acima para obter equações descrevendo a trajetória do ponto $A$ em termos de um único parâmetro $t$:

${\begin{array}{rcrcl}x&=&x_{c}+x'&=&(R-r)\cos t+\rho \cos {\frac {R-r}{r}}t,\\[4pt]y&=&y_{c}+y'&=&(R-r)\sin t-\rho \sin {\frac {R-r}{r}}t.\\\end{array}}$

(usando o fato que a função $\sin$ é ímpar).

É conveniente representar a equação acima em termos do raio $R$ de $C_{o}$ e parâmetros adimensionais descrevendo a estrutura do Espirógrafo. Vamos admitir

$l={\frac {\rho }{r}}$

e

$k={\frac {r}{R}}.$

O parâmetro $0\leq l\leq 1$ representa o quão longe o ponto $A$ está localizado do centro de $C_{i}$. Ao mesmo tempo, $0\leq k\leq 1$ representa quão grande o círculo interno $C_{i}$ é em relação ao externo $C_{o}$.

Observa-se agora que

${\frac {\rho }{R}}=lk,$

e portanto as equações de trajetória ficam com a forma de

${\begin{array}{rcl}x(t)&=&R\left[(1-k)\cos t+lk\cos {\frac {1-k}{k}}t\right],\\[4pt]y(t)&=&R\left[(1-k)\sin t-lk\sin {\frac {1-k}{k}}t\right].\\\end{array}}$

Parâmetro $R$ é um parâmetro de escala e não afeta a estrutura do Espirógrafo. Diferentes valores de $R$ iriam produzir semelhantes desenhos de Espirógrafo.

Os dois casos extremos $k=0$ e $k=1$ resultam em trajetórias degeneradas do Espirógrafo. No primeiro caso extremo, quando $k=0$, temos um círculo simples de raio $R$, correspondente ao caso onde $C_{i}$ foi contraído a um ponto. (Divisão por $k=0$ na fórmula não é um problema uma vez que $\sin$ e $\cos$ são funções limitadas).

O outro caso extremo $k=1$ corresponde ao raio $r$ do círculo interno $C_{i}$ coincidindo com o raio $R$ do círculo externo $C_{o}$, i.e. $r=R$. Neste caso a trajetória é um simples ponto. Intuitivamente, $C_{i}$ é muito grande para rolar dentro do círculo de mesmo tamanho $C_{o}$ sem derrapar.

Se $l=1$, então o ponto $A$ está na circunferência de $C_{i}$. Nesse caso as trajetórias são chamadas de hipocicloides e as equções acima reduzidas àquelas para um hipocicloide.

Estrela

A empresa Estrela lançou um produto similar com o nome de "Espirograf".

Ver também

• Epicicloide

Bibliografia

• Knight, John I. (6 September 2018). "Mechanics Magazine". Knight; Lacey.
• Goldstein, Cathérine; Gray, Jeremy; Ritter, Jim (1996). L'Europe mathématique: histoires, mythes, identités. Editions MSH. p. 293.

Ligações externas

• «Spirograph in Java» 
• Weisstein, Eric W. «Spirograph» (em inglês). MathWorld 
• «Spirograph Toy Collection»  - Collection with photos of many versions including UK and Australian issues.
• «Software Spirograph»  in Javascript und AFLAX/Flash
• «Spirograph source files in C#» 
• https://collection.sciencemuseum.org.uk/objects/co60094/spirograph-and-examples-of-patterns-drawn-using-it-spirograph
• Kaveney, Wendy. "CONTENTdm Collection : Compound Object Viewer". http://digitallibrary.imcpl.org.
• Linderman, Jim. "ArtSlant - Spirograph? No, MAGIC PATTERN!". http://artslant.com.
• "From The Boy Mechanic (1913) - A Wondergraph". http://marcdatabase.com.