Dimensão
Na física e na matemática, a dimensão de um espaço matemático (ou objeto) é informalmente definida como o número mínimo de coordenadas necessárias para especificar qualquer ponto dentro dela.[1][2][nota 1] Assim, uma reta tem uma dimensão de um (1) porque apenas uma coordenada é necessária para especificar um ponto nela – por exemplo, o ponto no 5 em uma reta numérica. Uma superfície como um plano ou a superfície de um cilindro ou esfera tem uma dimensão de dois porque duas coordenadas são necessárias para especificar um ponto nela – por exemplo, uma latitude e uma longitude são necessárias para localizar um ponto na superfície de uma esfera. O interior de um cubo, um cilindro ou uma esfera é tridimensional porque são necessárias três coordenadas para localizar um ponto dentro desses espaços.
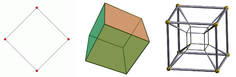

- Dois pontos pode ser conectado para criar um segmento de reta.
- Dois segmentos de linha paralela pode ser conectado para formar um quadrado.
- Dois quadrados paralelos pode ser conectado para formar um cubo.
- Dois cubos paralelos pode ser conectado para formar um tesserato.
Na mecânica clássica, espaço e tempo são categorias diferentes e referem-se a espaço e tempo absolutos. Essa concepção do mundo é um espaço de quatro dimensões, mas não o que foi considerado necessário para descrever o eletromagnetismo. As quatro dimensões do espaço-tempo consistem em eventos que não são absolutamente definidos espacial e temporalmente, mas são conhecidos em relação ao movimento de um observador. O espaço de Minkowski primeiro se aproxima do universo sem gravidade; as variedades pseudo-riemannianas da relatividade geral descrevem o espaço-tempo com a matéria e a gravidade. Dez dimensões são usadas para descrever a teoria das cordas, onze dimensões podem descrever a supergravidade e a teoria-M, e o espaço de estados da mecânica quântica é um espaço de função de dimensão infinita.
O conceito de dimensão não se restringe a objetos físicos. Espaços de alta dimensão frequentemente ocorrem na matemática e nas ciências. Eles podem ser espaços de parâmetros ou espaços de configuração, como na mecânica lagrangiana ou hamiltoniana; estes são espaços abstratos, independentes do espaço físico em que vivemos.
Na matemática editar
Na matemática, a dimensão de um espaço é o número de parâmetros necessários para identificar um ponto desse espaço.[nota 1]
Exemplos editar
- A dimensão de é , isto é, cada ponto de é descrito por números reais.
- A dimensão real de é , isto é, cada ponto de é descrito por números reais.
- A dimensão complexa de é , isto é, cada ponto de é descrito por números complexos.
- A dimensão de um espaço vectorial é o número de vectores de qualquer base desse espaço.
Contexto editar
É importante observar que a dimensão está vinculada à forma como o espaço se apresenta.
Assim, considerado como um espaço vetorial sobre os números reais , o espaço dos números complexos tem dimensão 2; considerado como um espaço vetorial sobre os números racionais , a sua dimensão é (a potência do contínuo).
Analogamente, é um espaço de dimensão 2 sobre , mas é um espaço de dimensão 4 sobre
Como outro exemplo, tome-se o espaço de Hilbert cuja base de Hilbert seja enumerável. No contexto dos espaços de Hilbert, ele tem, obviamente, dimensão , porém, visto como espaço vetorial, a sua dimensão é .
Espaços vetoriais editar
A dimensão de um espaço vetorial é o número de vetores em qualquer base para o espaço, ou seja, o número de coordenadas necessárias para especificar qualquer vetor. Essa noção de dimensão (a cardinalidade de uma base) é frequentemente chamada de dimensão de Hamel ou dimensão algébrica para distingui-la de outras noções de dimensão.
Para o caso não-livre, isso se generaliza para a noção do comprimento de um módulo.
Dimensão de Hausdorff editar
A dimensão de Hausdorff é útil para estudar conjuntos estruturalmente complicados, especialmente fractais. A dimensão Hausdorff é definida para todos os espaços métricos e, ao contrário das dimensões consideradas acima, também pode ter valores reais não inteiros.[3] A dimensão da caixa ou a dimensão de Minkowski é uma variante da mesma ideia. Em geral, existem mais definições de dimensões fractais que funcionam para conjuntos altamente irregulares e atingem valores reais positivos não inteiros. Os fractais se mostraram úteis para descrever muitos objetos e fenômenos naturais.[4][falta página][5][falta página]
Espaços de Hilbert editar
Todo espaço de Hilbert admite uma base ortonormal, e quaisquer duas dessas bases para um espaço particular têm a mesma cardinalidade. Essa cardinalidade é chamada de dimensão do espaço de Hilbert. Essa dimensão é finita se, e somente se, a dimensão de Hamel do espaço é finita e, nesse caso, as duas dimensões coincidem.
Na física editar
Na física, as dimensões são parâmetros utilizados para descrever os fenômenos observados. A física clássica descreve o espaço em três dimensões. A teoria da relatividade geral propõe uma geometria quadridimensional conhecida como espaço-tempo e teorias mais modernas sugerem a existência de dez ou onze dimensões.
Física clássica editar
A física clássica descreve o espaço usando três dimensões: grosseiramente falando, qualquer movimento pode ser decomposto em três componentes: cima/baixo, direita/esquerda e frente/trás. Mover-se para baixo significa deslocar-se no sentido negativo na direção vertical; mover-se para a esquerda equivale a deslocar-se no sentido negativo da direção horizontal e mover-se para trás significa deslocar-se negativamente na direção de topo.
Tempo editar
O tempo é muitas vezes chamado de quarta dimensão. Na física clássica e na percepção intuitiva humana, o tempo é visto como um parâmetro à parte das dimensões espaciais. Na teoria da relatividade, desenvolvida sobretudo pelos trabalhos de Henri Poincaré e Albert Einstein, o tempo é visto como uma das dimensões do espaço quadridimensional chamado de espaço-tempo.
Dimensões adicionais editar
A teoria das cordas e a teoria-M descrevem o universo com dez e onze dimensões, respectivamente.
Redes e dimensão editar
Algumas redes complexas são caracterizadas por dimensões fractais.[6] O conceito de dimensão pode ser generalizado para incluir redes incorporadas no espaço.[7] A dimensão caracteriza suas restrições espaciais.
Notas editar
Referências
- ↑ «Curious About Astronomy». Curious.astro.cornell.edu. Consultado em 3 de março de 2014. Arquivado do original em 11 de janeiro de 2014
- ↑ «MathWorld: Dimension». Mathworld.wolfram.com. 27 de fevereiro de 2014. Consultado em 3 de março de 2014. Cópia arquivada em 25 de março de 2014
- ↑ Fractal Dimension Arquivado em 2006-10-27 no Wayback Machine, Departamento de Matemática e Estatística da Universidade de Boston
- ↑ Bunde, Armin; Havlin, Shlomo, eds. (1991). Fractals and Disordered Systems. [S.l.]: Springer
- ↑ Bunde, Armin; Havlin, Shlomo, eds. (1994). Fractals in Science. [S.l.]: Springer
- ↑ Song, Chaoming; Havlin, Shlomo; Makse, Hernán A. (2005). «Self-similarity of complex networks». Nature. 433 (7024). Bibcode:2005Natur.433..392S. arXiv:cond-mat/0503078v1 . doi:10.1038/nature03248
- ↑ Daqing, Li; Kosmidis, Kosmas; Bunde, Armin; Havlin; Shlomo Havlin, Shlomo (2011). «Dimension of spatially embedded networks». Nature Physics. 7 (6). Bibcode:2011NatPh...7..481D. doi:10.1038/nphys1932
- ↑ Dicionário Eletrônico Houaiss de Língua Portuguesa 3.0 (2009). Espaço e Dimensão. [S.l.]: Objetiva Ltda
Leitura adicional editar
- Katta G Murty, "Systems of Simultaneous Linear Equations" (Capítulo 1 do Computational and Algorithmic Linear Algebra and n-Dimensional Geometry, Publicação Científica Mundial: 2014 (ISBN 978-981-4366-62-5).
- Edwin A. Abbott, Flatland: A Romance of Many Dimensions (1884) (Domínio público: Online version with ASCII approximation of illustrations no Project Gutenberg).
- Thomas Banchoff, Beyond the Third Dimension: Geometry, Computer Graphics, and Higher Dimensions, Second Edition, W. H. Freeman and Company: 1996.
- Clifford A. Pickover, Surfing through Hyperspace: Understanding Higher Universes in Six Easy Lessons, Oxford University Press: 1999.
- Rudy Rucker, The Fourth Dimension, Houghton-Mifflin: 1984.
- Kaku, Michio (1994). Oxford University Press, ed. Hyperspace, a Scientific Odyssey Through the 10th Dimension. [S.l.: s.n.] ISBN 0-19-286189-1
- Krauss, Lawrence M. (2005). Viking Press, ed. Hiding in the Mirror. [S.l.: s.n.] ISBN 0670033952