Norma (matemática)

Em matemática, uma norma consiste em uma função que a cada vetor de um espaço vetorial associa um número real não-negativo. O conceito de norma está intuitivamente relacionado à noção geométrica de comprimento.

Uma circunferência centrada na origem de $\mathbb {R} ^{2}$ relativa a três normas distintas

Definição

Dado um espaço vetorial $X$ sobre o corpo $\mathbb {K}$ dos números reais ou complexos, uma função $\|\cdot \|:X\to \mathbb {R} ^{+}$ é chamada de norma se, para quaisquer $x,y\in X$ e todo $\alpha \in \mathbb {K} :$

• $\|x\|=0\Leftrightarrow x=0_{_{X}}.$ Se esta condição não for atendida, a função será no máximo uma seminorma.
• $\|\alpha x\|=|\alpha |\|x\|$
• $\|x+y\|\leqslant \|x\|+\|y\|$ (desigualdade triangular)

Se o espaço vetorial $X$ tem uma norma, ele passa a ser chamado de espaço normado, e denotado por $\left(X,\|\cdot \|\right).$

Métrica e topologia induzida

Toda norma induz de forma natural uma métrica $d$ em $X$ cujos valores são dados por: $$d(x,y)=\|x-y\|\,.$$

Também induz uma topologia localmente convexa que é gerada por todas as bolas:

$$B(x_{0},r)=\{x\in X:d(x,x_{0})<r\},~~\forall \,x\in X,\forall \,r\in \mathbb {R_{+}}$$

Normas equivalentes

Duas normas $\|\cdot \|_{1}$ e $\|\cdot \|_{2}$ sobre o mesmo espaço vetorial $X$ são ditas equivalentes se existirem constantes reais positivas $C_{1}$ e $C_{2}\,(C_{1}\leqslant C_{2})$ tais que: $$C_{1}\|x\|_{1}\leqslant \|x\|_{2}\leqslant C_{2}\|x\|_{1}~~\forall \,x\in X$$

Quando duas normas são equivalentes, elas induzem a mesma topologia.

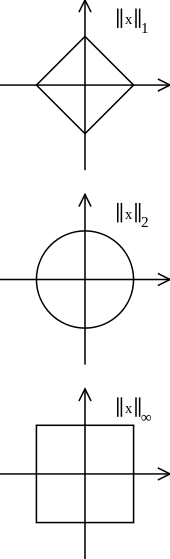
Normas em espaços de dimensão finita

Seja $x=\left(x_{1},x_{2},\ldots ,x_{n}\right)=\sum _{i=1}^{n}x_{i}e_{i}$ a representação de um vetor em $\mathbb {R} ^{n}$ ou $\mathbb {C} ^{n}.$

As normas canônicas definidas nestes espaços são as chamadas normas $\ell ^{p}$:

• $\|x\|_{p}={\Big (}\sum _{i=1}^{n}|x_{i}|^{p}{\Big )}^{\frac {1}{p}}~~,1\leqslant p<\infty$
• $\|x\|_{\infty }=\max _{i\in \{1,\ldots ,n\}}|x_{i}|$

O caso particular em que $p=2$ corresponde à norma euclidiana: $$\|x\|_{2}={\Big (}\sum _{i=1}^{n}|x_{i}|^{2}{\Big )}^{\frac {1}{2}}$$

Outras normas podem ainda ser definidas, no entanto, pode-se demonstrar que todas elas serão equivalentes.

Norma matricial

Ver artigo principal: Norma matricial

Se o espaço vetorial considerado é aquele formado pelas matrizes reais ou complexas de ordem $n\times m,$ denotado por $M^{n\times m},$ uma norma sobre esse espaço é chamada de norma matricial. Um exemplo de norma matricial é a norma 1, denotada $\|.\|_{1}$ definida como o máximo da soma módulo das entradas de cada linha, ou seja se $A=\left[a_{ij}\right]_{r\times s}$ então a norma 1 da matriz $A$ é o número não negativo dado por $$\|A\|_{1}=\max _{i\leqslant r}\sum _{j=1}^{s}|a_{ij}|.$$

A norma 1 da matriz $A={\begin{vmatrix}1&3\\2&-1\end{vmatrix}},$ por exemplo, é $$\|A\|_{1}=\max \left\{|1|+|3|,|2|+|-1|\right\}=\max \left\{4,3\right\}=4.$$

Normas em espaços de dimensão infinita

Espaços L^P

Ver artigo principal: Espaço Lp

As normas $\ell ^{p}$ têm análogos em alguns espaços de dimensão infinita.

Produto interno

Ver artigo principal: Produto interno

Se um espaço vetorial possui um produto interno, este pode definir uma norma, dada pelo produto interno do vetor com ele mesmo. $$\left\|v\right\|:={\sqrt {\langle v,v\rangle }}$$

Se uma norma provém de um produto interno, ela satisfaz a identidade do paralelogramo.

Referências

• SANTOS, José Carlos. Introdução à Topologia. Departamento de Matemática - Faculdade de Ciências da Universidade do Porto. Junho de 2010, 171 páginas. Disponível em: <http://www.fc.up.pt/mp/jcsantos/PDF/Topologia.pdf>. Acesso em: 12 jan. 2010. Página 60.
• Boldrini, José Luiz et. al. Álgebra Linear 3ª ed. [S.l.]: Harbra. p. 342 
• Lima, Elon Lages (1981). Curso de análise, Volume 2. Instituto de Matemática Pura e Aplicada. Rio de Janeiro: Instituto de Matemática Pura e Aplicada 

Ver também

• Produto interno
• Espaço de Banach
• Espaço euclidiano
• Espaço métrico
• Espaço vetorial topológico
• Funcional de Minkowski
• Semi-norma